教学内容 教科书第27页例1、“练一练”、第30页的练习五第1-4题。 教材分析 “三位数数乘两位数”隶属“数与代数”领域“数与运算”主题,运算能力是本单元的关键核心素养。在教材内容编排上,本单元是整数乘法学习的最后一个阶段,需要对整数乘法的算理和算法进行回顾与整理。大部分学生处于能正确笔算三位数乘两位数的学习起点,那“三位数乘两位数”这一内容最有利于在哪些方面培养人呢?本节课首先是培养学生的运算能力、推理意识、应用意识等数学核心素养,其次是培养学生类推迁移、整体建构的思维能力。基于此,教材在尊重学生的认知经验和基本技能的基础上,引导学生自主探索三位数乘两位数的笔算方法,让学生通过多次沟通比较经历知识的形成与发展过程,体验数学研究的方法。这样既能帮助学生掌握知识,也有利于深化学生的数学思维、完善学生的认知结构。 学生分析 学生在四年级下册学习笔算三位数乘两位数时,已经有了两、三位数乘一位数、两位数乘两位数的笔算经验,大部分学生已经“不学而会”,能正确笔算三位数乘两位数。 核心目标 核心素养:运算能力和数感 (1)理解三位数乘两位数的笔算算理,掌握三位数乘两位数的笔算算法,培养学生的运算能力 (2)利用已有知识自主解决多位数乘法笔算问题,发展迁移能力,培养学生的数感。 (3)在探索与交流的过程中感受迁移方法的魅力,体会探索数学的乐趣。 教学重点 掌握三位数乘两位数的笔算算法。 教学难点 理解三位数乘两位数的笔算算理,发展迁移能力。 学习任务设计 1.创设情境,激发兴趣 2.自主尝试,类比迁移 3.合作探究,深化理解 4.灵活运用,巩固升华 教学过程 一、创设情境,激发兴趣 师:我校有一位学生经常在大型活动的舞台上担任主持人。这一次他将代表我校参加全市的演讲比赛,这让他既高兴又忐忑,听一听他在忐忑什么? “我的语速是每分钟128个字,每个参赛选手演讲的时长为16分钟,我能将2100个字的稿子在规定时间内说完吗?” 师:谁能告诉大家他究竟遇到了什么困难? 学生积极寻找题目中的数学信息。 二、自主尝试,类比迁移 1.估算。 引导:是的,他遇到的问题是“能不能将2100个字的稿子在规定时间内说完”。你们觉得他能说完吗? 生:我认为解决这道题的关键是计算128×12的结果是多少。 提问:谁能估一估128×12 的结果是多少?说一说你的想法。 学生资源:生1:我把128估成100,100×16=1600;生2:我把16估成20,128×20=2560。 师:是啊,从大家估算的结果看,还是不能确定稿子能不能说完。那他在16分钟内究竟能说多少个字呢?现在我们一起在练习本上笔算128×16。 2.笔算。  学生独立完成,教师巡视指导并选取有代表性的学生作品进行展示: 学生独立完成,教师巡视指导并选取有代表性的学生作品进行展示:
提问:谁看懂了这位同学的作品? 生:他是先用16个位上的6去乘128的每一位得到768,再用16十位上的1去乘128的每一位得到128个十,最后把两个积加起来就得到结果2048。 引导:那竖式中算出来的768和128分别表示的含义是什么? 生:768是用16个位上的6去乘128得到的积,所以表示的是768个一,而128是用16十位上的1去乘128得到的积,所以表示的是128个十。 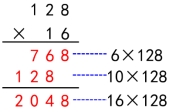 课件展示: 课件展示:
师:这就是三位数乘两位数的笔算过程。你们都没有学过,怎么一下子就计算出来了呢? 生1:我们以前学过两位数乘两位数,它们的计算方法差不多。 生2:我觉得和两位数乘两位数的计算方法应该是一样的。 师:我们以28×16为例回顾一下两位数乘两位数是怎样计算的。指名学生回顾,教师相机板书: 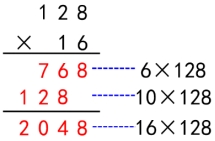 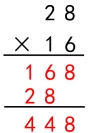
引导:对比这两个竖式,你发现了什么? 生1:都是先用第二个乘数个位上的数去乘第一个乘数,再用第二个乘数十位上的数去乘第一个乘数,最后相加两次得到的积即可得到最后的结果。 生2:乘数128多了一个百位,在乘的时候再多乘一下百位上的数就可以了。 师:同学们能够找到新旧知识之间的联系,把计算两位数乘两位数的经验迁移到新知上,真是太厉害了。其实,三位数乘两位数与两位数乘两位数的算理是一致的,这样他们算法也就一致了。 提问:谁能结合两位数乘两位数笔算的算法总结一下三位数乘两位数应该怎么算啊。 学生总结 明确算法:分别用两位数个位和十位上的数依次去乘三位数,用哪一位上的数去乘,乘得的数的末位就要和哪一位对齐,最后把两次乘得的积加起来。 【设计意图:学生结合已有的两位数乘两位数的知识经验,自主理解三位数乘两位数的算理,类推三位数乘两位数的算法。教师通过问题“你们都没有学过,怎么一下子就计算出来了呢”引导学生寻找新旧知识之间的联系。接着举例进行对比,引发学生的深度思考,让不同思维层次的学生都认识到三位数乘两位数与两位数乘两位数的算法一致,从而将模糊的感觉提升为清晰的认知,将运算技能与推理等思维能力的培养有机结合在一起,初步感知笔算乘法知识的内在联系。】 3.验算。 师:我们在计算时通常会验算,你们知道验算的方法都有什么吗? 生:再计算一遍或者交换位置变成两位数乘三位数。 师:现在我们尝试运用交换位置的方法来验算一下,看一看计算结果是否正 确。同学们可以在练习本上自主练习。学生自主列式计算,教师巡视指导并  选取有代表性的学生作品进行展示: 选取有代表性的学生作品进行展示:
师:谁能看懂这位同学是怎么计算的? 生:先计算8 个一×16=128 个一,再计算2个十×16=32个十,继续计算1个百×16=16个百,最后相加即可得到结果是2048。 师:明明都是128 和16的积,为什么中间的积有时是两层,有时又是三层呢? 生1:因为两个乘数交换了位置。 生2:第二个乘数是两位数,中间的积就有两层;第二个乘数是三位数,那么中间的积就有三层。 生3:我们在计算时是用第二个乘数每一位上的数依次去乘第一个乘数,所以第二个乘数是几位数乘出来的积就有几层。 师:真是一群爱思考问题的好孩子。 你们也没有学习过两位数乘三位数,怎么就会计算了呢? 生:我们只是把之前的经验迁移到了这里。 【设计意图:教师强调对乘法运算结果进行验算,以保证结果的正确性,培养学生良好的学习习惯。虽然学生能初步感知到笔算整数乘法的算理和算法的统一,但缺乏深刻领悟,于是教师通过辨析两位数乘三位数的笔算过程,沟通运算之间的联系,促使学生对整数乘法的笔算方法有了更清晰的认识,逐步发现整数乘法运算的本质。】 三、合作探究,深化理解  课件出示: 课件出示:
师:其实老师还带来了一种古代欧洲人的算法,计算过程足足有6层,你们能看懂吗?同桌之间讨论交流。 生:古代欧洲人的算法是每计算一步就记录一次,而我们今天这节课的算法将它的前三步、后三步分别合并成了一步。 师:仅听语言描述很抽象,我们可以把两个算式放在一起对比观察。 生:这两个算式都是用第二个乘数每一个数位上的数依次去乘128的每一位,算法一样,只是记录的方式不一样。 师:是的,其实计算方法是一样的,只不过我们这节课探究出的记录方法比较简洁。 【设计意图:学生学会计算三位数乘两位数后,教师引导学生对比古代欧洲的算法和今天的算法,不仅带领学生经历了知识的发展过程,还和学生一起发现两种算法的本质都是先算出分别有多少个计数单位,然后再求和。这样做,既让学生学会怎样算,还深刻认识到为什么这样算,更了解到相关数学史和知识进步的不易。】 四、灵活运用,巩固升华 1.判一判。 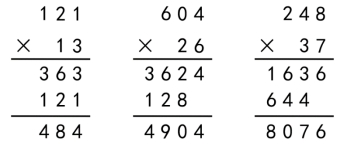
①数位没有对齐 ②积有0,没有写0占位 ③加错进位的数 2.算一算。 六一儿童节庆典支出清单 
师:我们学习计算是为了解决生活中的实际问题。六一儿童节,学校正在筹备庆典活动,这是活动的道具支出清单,你们能计算出一共需要多少元吗? 生:列式是2132×24。 师:这是一道四位数乘两位数的算式,你们能计算出结果吗?在练习本上自主完成。 学生独立完成,教师收集并展示有代表性的学生作品。 师:(边指边说)我们看一下这几位同学的计算过程,他们都做对了吗? 生:都做对了。 师:四位数乘两位数你们也没学过,怎么也会做呢? 生:其实计算方法都是一样的,只是在乘的时候又多乘了一下千位上的数。 师:真是太好了,现在又把计算方法迁移到了四位数乘两位数 【设计意图:教师引导学生通过解决生活中的实际问题唤醒应用意识,为后面对数量关系“单价×数量=总价”的学习做好铺垫。同时,再次引导学生迁移经验自主计算四位数乘两位数,沟通了知识的内在联系,提升了学生的思维能力、运算能力。运算能力不仅是一种正确计算的技能,也是一种基于深度理解的应用意识,更是影响学生长远发展的基本素养。】 3.编一编。 你们没有学过刚才的算式,但都能计算出来,如果换成是四位数乘三位数、五位数乘五位数,你们还会计算吗?课后,请同学们根据活动要求独立完成。 活动要求: (1)写一写:写出一个多位数乘多位数的算式。 (2)算一算:用竖式笔算出结果。 (3)验一验:同桌之间用计算器进行验算。 【设计意图:】教师通过编一编引导学生沟通整数乘法笔算方法之间的联系,让学生反思感悟到不管是几位数乘几位数,计算的道理都是一样的。】 五、课堂总结,梳理提升 通过本课的学习,你有什么收获? 还有哪些疑问? 板书设计 三位数乘两位数的笔算 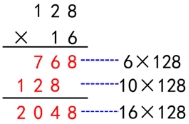
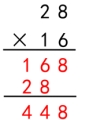
|